BCD

 Código BCD

Binary-Coded Decimal o Decimal Codificado Binario, es un estándar para representar números decimales en el sistema binario, en donde cada dígito decimal es codificado con una secuencia de 4 bits.

Con esta codificación especial de los dígitos decimales en el sistema binario, se pueden realizar operaciones aritméticas como suma, resta, multiplicación y división de números en representación decimal, sin perder en los cálculos la precisión ni tener las inexactitudes en que normalmente se incurren con las conversiones de decimal a binario puro y de binario puro a decimal.

En BCD cada cifra que representa un dígito decimal (0, 1,...8 y 9) se representa con su equivalente binario en cuatro bits (nibble o cuarteto) (esto es así porque es el número de bits necesario para representar el nueve, el número más alto que se puede representar en BCD).


Ejemplos de conversión de Decimal a código BCD

Ejemplo 1: La conversión directa típica del número decimal 85 a binario es: 8510 = 10101012.

La representación del mismo número decimal en BCD se muestra en la siguiente imagen.

85 decimal a Código BCD (Decimal Codificado en Binario)

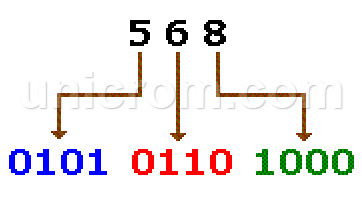
Ejemplo 2: La conversión directa típica del número decimal 568 a binario es: 56810 = 10001110002.

La representación del mismo número decimal en BCD se muestra a la siguiente imagen.

568 decimal en código BCD (Decimal Codificado en Binario)

Uso

Este sistema de numeración es demasiado común en el ámbito de sistemas electrónicos ya que esta area debe mostrar un valor numérico y BCD ayuda.
Por ejemplo en los sistemas digitales no programados:

  • microprocesador 
  • microcontrolador

BCD simplifica el uso de datos numéricos que deben ser mostrados en por ejemplo, un visualizador de 7 segmentos, lo cual a su vez trae simplificación en el diseño físico del circuito.

Ventajas

  • Simplemente se debe memorizar el equivalente en binario de los números decimales del 0-9
  • No existe límite para tamaño de un número

Desventajas

  • Suma y resta tienen reglas diferentes
  • Requiere de más bits que en binario para mostrar un número decimal



https://unicrom.com/codigo-bcd-decimal-codificado-en-binario/

https://www.ecured.cu/C%C3%B3digo_BCD

http://arquiconsamuel.blogspot.com/2017/08/codigo-bcd.html

Comentarios

Publicar un comentario

Entradas populares de este blog

ARREGLO LOGICO GENERICO (GAL)

Imagen
   JAVIER MICHEL FLORES COYOTL   GAL  GAL (Generic Array Logic), en español Arreglo Lógico Genérico, son un tipo de circuito integrado, de marca registrada por Lattice Semiconductor, que ha sido diseñados con el propósito de sustituir a la mayoría de las PAL, manteniendo la compatibilidad de sus terminales. Utiliza una matriz de memoria EEPROM en lugar por lo que se puede programar varias veces. Un GAL en su forma básica es un PLD con una matriz AND reprogramable, una matriz OR fija y una lógica de salida programable mediante una macrocelda. Esta estructura permite implementar cualquier función lógica como suma de productos con un número de términos definido. En los PLDs no reprogramables la síntesis de las ecuaciones lógicas se realiza mediante quema de fusibles en cada punto de intersección de los pines de entrada con las compuertas. En el caso de un GAL es básicamente la misma idea pero en vez de estar formada por una red de conductores ordenados en filas y col...
Leer más

Función "rising_edge" para VHDL

Esta instrucción detecta el flanco ascendente de una  señal  std_ulogic   o  std_logic .  Devolverá verdadero cuando la señal cambie de un valor bajo (  '0' o  'L' ) a un valor alto (  '1' o  'H' ). Ejemplo En este ejemplo, el simulador ejecuta el cuerpo del  if  exactamente una vez por ciclo de reloj, en el flanco ascendente de la señal de reloj. signal clock : std_logic; ... sync_stuff: process (clock) begin if rising_edge(clock) then ... end if; end process; En pocas palabras, cuando detecta un 1 nos devolvera un 1 y si no detecta nada no nos devolvera ningun valor. Referencia The rising_edge function . (s. f.). Computing Science - Simon Fraser University.  https://www2.cs.sfu.ca/~ggbaker/reference/std_logic/1164/rising_edge.html
Leer más

Señal del reloj en VHDL

En los sistemas digitales el reloj es el elemento que marca el sincronismo entre todos los elementos del circuito. Cada vez que hay un cambio, normalmente de 0 a 1, del reloj, los elementos de memoria, llamados biestables o flip-flops se cargan con los nuevos datos calculados durante el periodo transcurrido entre el cambio anterior y el actual. El tiempo que tarde la señal en llegar de su origen a su destino entre dos pulsaciones de este corazón eléctrico, lo denominamos el  camino crítico del circuito , y es la velocidad máxima a la que puede latir el reloj, ya que si fuera más rápido las señales no serían estables a las entradas de los flips-flops y el circuito comenzaría a dar resultados erróneos. library IEEE; use IEEE.STD_LOGIC_1164.ALL; entity clk_div is generic (divider : integer range 0 to 1023); port ( clk_i : in std_logic; clk_o : out std_logic Bibliografía: vhdl_es. (2019, 5 de febrero).  Dividir el reloj en una FPGA - VHDL.es . VHDL.es....
Leer más